No sé si us ha passat mai que un llibre o pel·lícula us hagi ajudat a prendre decisions importants o a introduir canvis a la vostra vida. A mi sí, i en més d'una ocasió. L'última ha sigut després de llegir el llibre La màgia de l'ordre de Marie Kondo, on l'autora ens explica un mètode per ordenar un espai i mantenir-lo ordenat. Si ha venut més de 3 mil·lions d'exemplars, penso que és perquè el seu contingut cobreix una necessitat fins ara no coberta: aprendre a organitzar i relacionar-se amb un espai de manera pràctica i eficaç i amb sentit.
Després de llegir-lo he anat reorganitzant els espais on passo més temps i realment cada vegada m'hi trobo millor. L'harmonia de l'espai transmet benestar.
Després de llegir-lo he anat reorganitzant els espais on passo més temps i realment cada vegada m'hi trobo millor. L'harmonia de l'espai transmet benestar.
El que no sé si haurà pensat algú en llegir el llibre és el símil que es pot fer entre ordenar un espai i ordenar la informació que emmagatzemem al cervell. Mentre el llegia jo vaig pensar en com desem la informació de matemàtiques quan anem aprenent.
L'espai, casa o despatx del que parla el llibre seria el nostre cervell i els objectes que desem i ordenem serien els conceptes i mètodes que aprenem.
En el seu llibre, Marie Kondo aconsella no guardar un mateix tipus d'objecte en espais diferents i usar separacions per agrupar-los. En matemàtiques, si no agrupem un concepte de matemàtiques en un mateix espai pot ser complicat i lent accedir a la informació relativa a aquest concepte.
Imagineu-vos que necessiteu unes sabates esportives concretes i aneu a uns grans magatzems a comprar-les. Si totes les botigues de sabates estiguessin a la mateixa planta, i cada botiga tingués només un tipus de sabata, esportives, sabatilles, ... aniríeu molt ràpid en trobar el que busqueu perquè només hauríeu d'anar directament a la botiga de sabates d'esport.
En canvi, si hi hagués botigues de sabates a cada planta, i a cada botiga hi hagués sabates de tot tipus, hauríeu de recórrer més d'una botiga de sabates i fins i tot, potser totes, per trobar les que busqueu. Doncs és la mateixa situació.
Si estudiem la informació sense crear relacions i lligams entre els conceptes, és com si estiguéssim construïnt moltes botigues de sabates, que no tenen ni telèfon, ni Internet, ni accés de cap tipus a les altres botigues. Quan volem accedir a la informació, hem de recórrer més circuits neuronals (botigues) per trobar-la.
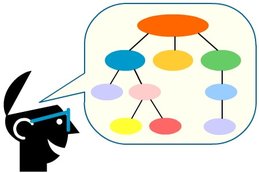
Per això és important fer esquemes per resumir i donar una estructura al que aprenem. Per fer-ho podem plantejar-nos preguntes del tipus: en quin ordre m'estan donant la informació? És un ordre cronològic? Perquè han creat aquests diferents apartats? N'hi podria haver més? Cada apartat és un mètode diferent? Tots s'apliquen al mateix cas? Això que m'expliquen es pot fer sempre? Des de quan se sap? Qui ho va descobrir?...
Així és com s'aprèn, s'aprèn a pensar, s'entén que el que ens ensenyen no ha sortit del no res, que hi ha hagut una cadena de pensaments i una evolució que ha portat a aquest coneixement i que pot ser assequible quan es segueixen els passos lògics necessaris.
Animeu els alumnes a fer esquemes o el que ara s'anomena mapa mental, que encara que sembla nou, era utilitzat ja en la Grècia antiga. O encara millor, perquè els professors no feu un mapa mental abans d'iniciar el curs, o un capítol, o una classe? Tot això facilita que els alumnes es situin, sàpiguen on són i cap on van dins de la gegantina xarxa que constitueix l'aprenentatge.
L'espai, casa o despatx del que parla el llibre seria el nostre cervell i els objectes que desem i ordenem serien els conceptes i mètodes que aprenem.
En el seu llibre, Marie Kondo aconsella no guardar un mateix tipus d'objecte en espais diferents i usar separacions per agrupar-los. En matemàtiques, si no agrupem un concepte de matemàtiques en un mateix espai pot ser complicat i lent accedir a la informació relativa a aquest concepte.
Imagineu-vos que necessiteu unes sabates esportives concretes i aneu a uns grans magatzems a comprar-les. Si totes les botigues de sabates estiguessin a la mateixa planta, i cada botiga tingués només un tipus de sabata, esportives, sabatilles, ... aniríeu molt ràpid en trobar el que busqueu perquè només hauríeu d'anar directament a la botiga de sabates d'esport.
En canvi, si hi hagués botigues de sabates a cada planta, i a cada botiga hi hagués sabates de tot tipus, hauríeu de recórrer més d'una botiga de sabates i fins i tot, potser totes, per trobar les que busqueu. Doncs és la mateixa situació.
Si estudiem la informació sense crear relacions i lligams entre els conceptes, és com si estiguéssim construïnt moltes botigues de sabates, que no tenen ni telèfon, ni Internet, ni accés de cap tipus a les altres botigues. Quan volem accedir a la informació, hem de recórrer més circuits neuronals (botigues) per trobar-la.
Per això és important fer esquemes per resumir i donar una estructura al que aprenem. Per fer-ho podem plantejar-nos preguntes del tipus: en quin ordre m'estan donant la informació? És un ordre cronològic? Perquè han creat aquests diferents apartats? N'hi podria haver més? Cada apartat és un mètode diferent? Tots s'apliquen al mateix cas? Això que m'expliquen es pot fer sempre? Des de quan se sap? Qui ho va descobrir?...
Així és com s'aprèn, s'aprèn a pensar, s'entén que el que ens ensenyen no ha sortit del no res, que hi ha hagut una cadena de pensaments i una evolució que ha portat a aquest coneixement i que pot ser assequible quan es segueixen els passos lògics necessaris.
Animeu els alumnes a fer esquemes o el que ara s'anomena mapa mental, que encara que sembla nou, era utilitzat ja en la Grècia antiga. O encara millor, perquè els professors no feu un mapa mental abans d'iniciar el curs, o un capítol, o una classe? Tot això facilita que els alumnes es situin, sàpiguen on són i cap on van dins de la gegantina xarxa que constitueix l'aprenentatge.
Així tindran una estructura clara dels conceptes i no se sentiran tant perduts. Bones explicacions i ben estructurades van creant dins seu un sentiment fort de lògica i sentit que facilita la comprensió de l'estructura matemàtica i, de la mateixa manera que aconsegueix la Marie Kondo, aconsegueixen produir benestar i un aprenentatge fluit.
Gràcies Marie.
Gràcies Marie.



 RSS Feed
RSS Feed
